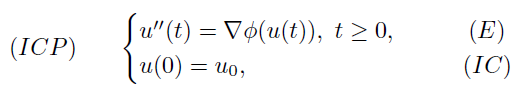BOUNDED SOLUTIONS FOR AN INCOMPLETE CAUCHY PROBLEM INVOLVING A NON-CONVEX FUNCTION

Gheorghe Moroșanu^†, Cristian Vladimirescu^‡

Abstract: Consider in a real Hilbert space (H, (·, ·), | · |) the following incomplete Cauchy problem,

where u₀ ∈ H is a given initial state, and ϕ : H → ℝ is a C¹, nonconvex function (preferably quasiconvex, as explained below). We call (ICP) an incomplete Cauchy problem because the usual additional Cauchy condition u’(0) = v₀ is missing. In this paper, we establish sufficient conditions on the non-convex function ϕ guaranteeing the existence of bounded solutions on [0, ∞) of (ICP) for any u₀ ∈ H.

Keywords: second order differential equation, gradient of a C¹function, bounded solutions.

MSC: 34G20, 26B25.
More …

DOI 10.56082/annalsarscimath.2026.1.217

^†gheorghe.morosanu@ubbcluj.ro, Department of Mathematics, Babeș-Bolyai University, Cluj-Napoca, Romania & Academy of Romanian Scientists, Bucharest
^‡cristian.vladimirescu@edu.ucv.ro, Computers and Information Technology Department, University of Craiova, Craiova, Romania

PUBLISHED in

Annals Academy of Romanian Scientists Series on Mathematics and Its Application,

Volume 18 no 1, 2026

ISSN ONLINE 2066 – 6594
ISSN PRINT 2066 – 5997